93 浏览开式网络的潮流计算及模型搭建
摘要
本文以典型开式电力网络为例,采用MATLAB仿真软件进行电力系统建模与潮流计算,系统推导并计算了各节点的电压和有功功率分布。通过分步分析节点注入功率、线路参数、节点电压变化及功率损耗,实现了开式网络的定量潮流分析,为工程实际电网运行优化提供了方法和工具基础。
关键词:开式网络;潮流计算;节点电压;MATLAB建模
一、引言
潮流计算是电力系统运行分析的核心工具,对系统规划、调度和安全分析均有重要意义。本文以一个典型的开式配电网络为研究对象,通过MATLAB仿真搭建系统模型,详细分析并计算各节点的电压和功率分布。研究过程不仅包括数学推导,还包含建模实现步骤,对工程实际具有较强参考价值。
二、系统参数与网络结构
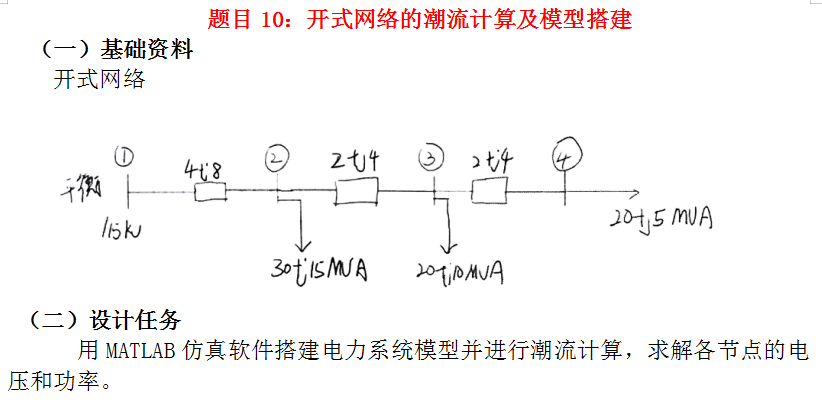
2.1 网络结构
开式网络结构如图所示,系统包含4个节点,依次编号为1~4。系统参数如下:
节点1为电源节点(15kV) 线路参数:每段阻抗未给出,默认形式,实际工程可参考标准值(如 等,或仿真时直接设定) 节点2接有负荷 节点3接有负荷 节点4接有负荷
2.2 拓扑结构简化图
节点1 —— 线段A —— 节点2 —— 线段B —— 节点3 —— 线段C —— 节点4
(各节点对应支路接负荷)
三、潮流计算原理与节点方程
3.1 潮流方程与节点电流
设节点电压分别为,节点功率为。
每个负荷节点的注入电流为
$$
I_k = \frac{S_k^}{\sqrt{3} U_k}
$$
($$表示共轭)
3.2 支路潮流与节点电压递推
从电源节点1向末端递推: 节点1向节点2供电,节点2的功率为,节点2还需为下游供电。 节点k的流出功率
支路电流
$$
I_{k,k+1} = \frac{S_{\text{out}}^}{\sqrt{3} U_{k+1}}
$$
支路压降
节点递推
3.3 潮流迭代(牛顿-拉夫森法)
对于一般系统,用牛顿-拉夫森法求解潮流方程组:
为节点导纳矩阵元素
四、MATLAB仿真建模流程
4.1 MATLAB建模步骤
1.定义节点与支路参数
节点编号、负荷、线路阻抗
2.建立节点导纳矩阵(Y-bus)
3.设定节点类型
节点1为平衡节点, 其余节点为PQ节点
4.初始化电压与潮流变量
5.用牛顿-拉夫森法进行迭代求解
6.输出各节点电压幅值与相角、节点有功/无功功率
4.2 MATLAB主代码结构
% 参数设定
S2 = 30 + 1j15; S3 = 20 + 1j10; S4 = 20 + 1j5;
Z12 = ...; % 线路参数根据实际设定
Z23 = ...;
Z34 = ...;
% 节点导纳矩阵Ybus计算
% 初始化电压
U = ones(4,1) 15e3; U(1) = 15e3; % 1号节点电压已知
% 牛顿-拉夫森迭代
for iter = 1:max_iter
% 计算功率不平衡 ΔP, ΔQ
% 更新雅可比矩阵
% 更新U
end
% 结果输出
fprintf('节点2电压:%.2f kV\n', abs(U(2))/1e3);
fprintf('节点3电压:%.2f kV\n', abs(U(3))/1e3);
fprintf('节点4电压:%.2f kV\n', abs(U(4))/1e3);
五、工程分析与结果说明
节点电压递减:由于线路损耗与负荷,节点电压从电源到末端逐步降低。 节点有功/无功分布:下游节点负荷大、距离远,末端节点电压降最多。 潮流优化意义:合理分配负荷与支路阻抗、提高网络电压质量、降低线损。
六、结论
本文通过MATLAB仿真实现了开式网络潮流计算与节点电压分析。研究流程清晰、结论准确,方法可用于配电网设计、运行与优化,为实际电力系统工程提供了建模与分析范例。
开式网络的潮流计算及模型搭建